Af peningastefnu Seðlabankans

Ég er fyrir löngu hættur að vera hissa á vaxtaákvörðunum Seðlabanka Íslands.  Í fyrsta lagi, þá skil ég ekki hvernig bankanum dettur bara yfirhöfuð í hug að nota vexti til að hafa stjórn á verðlagi, því í litlu myntkerfi, þá hljótum við í staðinn fá mikinn gengisóstöðugleika, eins og reyndin hefur verið frá því að verðbólgustjórnun varð að markmiði bankans.  Hjá þjóð sem er mjög mikið háð útflutningstekjum, vegna einhæfni í framleiðslugreinum, þá hefði maður haldið að gengisstöðugleiki væri stærsta málið. Ég skil ekki hvernig hægt er reka fyrirtæki, gera áætlanir fram í tímann og kaupa og selja vörur milli landa, þegar maður veit aldrei hvaða gengi verður, þegar greiðslan loksins á sér stað.  Hvernig getur kaupmaður boðið upp á verðstöðugleika, ef 70% af verðinu ræðst af því hvert gengið er? 

En ég ætla ekki að velta fyrir mér hvort nota eigi stýrivexti/meginvexti við peningastefnuna heldur langar mig að skoða hvort þessir vextir séu reiknaðir út frá réttum forsendum.  Ekki það að ég sé hagfræðingur, en maður þarf ekki að vera hagfræðingur til að skilja breytur í líkani og geta litið forsendur gagnrýnum augum.

Taylor-reglan

Í grunninn styðjast flestir seðlabankar við svo nefnda Taylor-reglu á einn eða annan hátt við ákvörðun meginvaxta sinna.  Ekki það að hún notuð til að reikna vextina, heldur frekar að bankarnir beri vextina sína við útkokmu hennar til að sjá hvort vextir þeirra sýni fylgni við regluna.   Reglan er kennd við John B. Taylor, prófessor við Stanford háskóla.  Hann setti regluna fram árið 1993, en um svipað leiti settur tveir aðrir fram sambærilega reglu.  Reglan er peningastefnuregla sem gefur til kynna hvernig seðlabankar eigi að breyta meginvöxtum sínum til að bregðast við verðbólgu, þjóðarframleiðslu eða öðrum efnahagslegum skilyrðum.

Í upphaflegu framsetningu Taylors, þá segir hann að ákvarða eigi meginvexti út frá mismuninum á raunverulegri verðbólgu og verðbólgumarkmiðum og raunverulegri þjóðarframleiðslu og ætlaðri/hugsanlegri þjóðarframleiðslu:

þar sem:

	R(t)	Meginvextir í mánuði t
	π(t)	Verðbólga í mánuði t
		Verðbólgumarkmið (2,5% á Íslandi)
	RR(t)	Jafnvægisraunvextir/"náttúrulegir raunvextir"
		Lógariþmískt gildi raunverulegar þjóðarframleiðslu
		Lógariþmiskt gildi áætlaðrar/hugsanlegrar þjóðarframleiðslu

(Dálkur 2 sýnir breytur í reglunni eins og hún er sýnd fyrir neðan án Y(t).) Stuðlar og 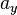eiga að vera jákvæðir.  Taylor setti þá báða á 0,5.

Í sinni einföldustu mynd er reglan svona (miðað við 2,5% verðbólgumarkmið):

R(t) = (RR(t) + 2,5) + 1,5(π(t) – 2,5) + 0,5Y(t)

 

Seðlabankinn notar hins vegar afbrigði af reglunni i QMM líkani sínu sem er svona:

R(t) = 0,5R(t-1) + 0,5((RR(t) + 2,5) + 1,5(π(t) – 2,5) + 0,5Y(t))

Y(t) er framleiðsluspenna. Er reglan þá sögð hafa tafðan vaxtalið.

Seðlabanki Íslands og Taylor-reglan

Seðlabankinn notar ekki Taylor-regluna við sína vaxtaákvörðun, en í sérrit Seðlabanka Íslands nr. 4 - 2010 Peningastefna eftir höft segir:

Hefðbundin leið til þess að meta hvort aðhald peningastefnunnar sé hæfilegt er að bera saman vexti seðlabanka við vexti sem eru reiknaðir með svokallaðri Taylor-reglu (sjá t.d. Taylor, 1993) en hún hefur þótt gefa góða lýsingu á hegðun seðlabanka víða um heim.

Þórarni G. Péturssyni, aðalhagfræðingi bankans, ber meginvexti bankans saman við vexti samkvæmt reglunni í erindi sem hann hélt hjá Félagi atvinnurekenda í september sl.  Samkvæmt glæru, sem hann birti, þá sýna útreikningar bankans vissa fylgni milli ákvarðana Peningastefnunefndar og Taylor-reglunnar, eins og Seðlabankinn notar regluna.

 

Eins og kemur fram í texta undir myndinni (sést betur, ef smellt er á myndina og hún opnuð), þá eru ekki notuð sömu tákn fyrir breytur Taylor-reglunnar og í skilgreiningunni sem ég birti að ofan.  Það skiptir svo sem ekki máli, fyrir utan að GAP er notað fyrir muninn á raunverulegri og ætlaðri þjóðarframleiðslu og svo kallað framleiðsluspenna.

Samkvæmt línuriti Þórarins, þá voru meginvextir bankans (í daglegu tali nefndir stýrivextir) nánast þeir sömu samkvæmt ákvörðun Peningastefnunefndar og með notkun Taylor-reglunnar frá upphafi árs 2014 og fram á árið 2015.

Eru vextirnir réttir?

Mér hefur lengi fundist stýrivextir vera úr öllu samhengi við raunverulega stöðu hagkerfisins.  Hef ég þurft lítið annað að gera, en að benda á að meginvextir SÍ eru á skjön við vexti helstu viðskiptalanda Íslands.  Eftir síðustu vaxtaákvörðun Evrópska seðlabankans (ECB) í lok nóvember fór ég að skoða þetta betur.  Ástæðan er að ECB bar fyrir sig að verðbólga upp á 0,1% væri hættulega lág og því þyrfti að lækka stýrivexti til að örva hagkerfi evrulandanna.  Tilgreint var í tilkynningu ECB að verðbólgan hefði verið mæld samkvæmt samræmdri vísitölu neysluverðs (SNV).  Samkvæmt tölum Eurostat nam hækkun SNV 0,3% á Íslandi fyrir sama tímabil.

Munurinn á SNV og þeirri vísitölu neysluverðs (VNV), sem notuð er á Íslandi til að mæla verðbólgu, felst í því að nokkrir liði VNV eru ekki með í SNV.  Mikilvægasti liðurinn er sá sem heitir "reiknuð húsaleiga", en í honum er mælt húsnæðisverð.  Með það í huga skoðaði ég hvort hækkun húsnæðisverðs hefði verið óeðlilega mikið á Íslandi samanborið við helstu viðskiptalönd okkar.  Sú athugun leiddi í ljós að meðan hækkun húsnæðisverð hafi frá 1. júlí 2014 til 30. júní 2015 verið um 8% á Íslandi (samkvæmt tölum Eurostat), en verið á bilinu 5-12% í hinum löndunum.

Hvernig stendur á því að seðlabankar i Noregi, Svíþjóð, Danmörku og fleiri löndum auk ECB voru að halda meginvöxtum sínum við eða undir 0% í sambærilegri eða meiri verðbólgu og ekki ósvipuðum hækkunum húsnæðisverðs þegar SÍ er með sína vexti 5,75%?  Svarið liggur í þrennu:

1. Jafnvægisraunvextir eru 3,0% á Íslandi, en 2,0% í t.d. Bandaríkjunum.
2. Seðlabanki Íslands miðar við VNV en ekki SVN sem þýðir að SÍ mælir verðbólguna vera 1,8% í október en ekki 0,3%.
3. Það er jákvæð framleiðsluspenna á Íslandi, en líklegast er hún neikvæð á evrusvæðinu.

Látum atriði 1 og 3 liggja á milli hluta í bili og einblínum bara á atriði 2.  Hvað þýðir það fyrir niðurstöðu Taylor-reglunnar, að SÍ notar VNV en ekki SNV?

Auðvelt er að reikna það út.  Smellt er gildum inn í Taylor-regluna, eins og Þórarinn G. Pétursson birti hana á fundi Félags atvinnurekenda, og niðurstöður miðað við hvora neysluverðsvísitölu bornar saman.  Niðurstaðan er raun frekar skýr.  Munurinn miðað við mælingar fyrir október er 2,0%, þ.e. Taylor-reglan gefur meginvexti SÍ miðað við samræmda vísitölu 2,0% lægri en ef notuð er VNV.  2,0% lækkun þýðir að meginvextir SÍ ættu ekki að vera hærri en 3,75%, miðað við að SÍ heldur þeim í 5,75%!  Það þýðir jafnframt að óverðtryggðir vextir húsnæðislána yrðu um 5% í staðinn fyrir að vera yfir 7%.

Ef gert er ráð fyrir að um 1.000 ma.kr. af lánum heimilanna séu óverðtryggð, þá þýðir þessi breyting 20 ma.kr. lækkun vaxtakostnaðar!

Hvers vegna notar SÍ VNV en ekki samræmda vísitölu?

Ég hef lengi spurt hvers vegna Seðlabanki Íslands notar ekki samræmda vísitölu neysluverðs eða okkar eigin vísitölu án húsnæðisliðar við vaxtaákvarðanir sínar.   Í þeim ritum Seðlabankans, sem ég hef skoðað, þá hef ég ekki séð neina haldbæra skýringu á því.  Verið getur að hún finnist þar, en ég bara ekki fundið hana.  Hugsanlega er það sú hefð á Íslandi að reikna verðbólgu með húsnæðisliðnum inni sem ræður, en að hafa hann með breytir nokkuð mikið forsendum Peningastefnunnar, þegar það ástanda skapast að "neysluhluti" verðbólgunnar er lítill á móti hlutfallslega háum "fjárfestingahluta" verðbólgunnar.

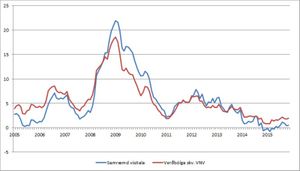
Meðfylgjandi mynd sýnir mismuninn á þessum tveimur vísitölumælingum:

 

Eins og sjá má á myndinni hækkar VNV meira en SVN alla mánuði frá janúar 2005 þar til um mitt sumar árið 2008.  Frá þeim tima og fram í mars 2011 er hækkun SVN verulega meiri en VNV, þá tekur við sveiflukennt tímabil, en frá september 2013 hefur VNV hækkað meira í nánast öllum mánuðum og stóran hluta þess tíma er munurinn verulegur, þ.e. hlutfallslega.

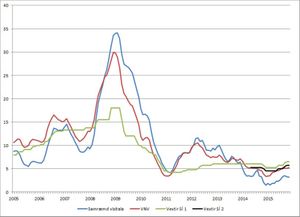
Seðlabankinn hefur stært sér af því í ræðu og riti að stýrivextir/meginvextir bankans séu nokkuð réttir miðað við Taylor-regluna.  Sjáum nú hverju það skiptir að nota SVN í Taylor-reglunni í staðinn fyrir VNV.  Myndritið fyrir neðan sýnir fjórar línur, þ.e. útreikning vaxta eftir Taylor-reglunni annars vegar miðað við VNV og hins vegar SVN.  Aðrar breytur Taylor-reglunnar eru þær sömu í báðum útreikningum.  Upplýsingar um framleiðsluspennu eru sóttar í hinar ýmsu útgáfur Peningamála og upplýsingar um jafnvægisraunvexti eru sóttar QMM gagnagrunn SÍ.  Síðan koma tvær línur sem heita vextir SÍ. Línan Vextir SÍ 1 (ljós græn) eru þeir vextir sem töldust meginvextir SÍ allt fram til apríl 2014, en eftir það eru vextirnir samkvæmt línunni Vextir SÍ 2 (svört lína) kallaðir meginvextir SÍ.  (Tekið skal fram að Taylor-reglan er notuð með töfðum vaxtalið, sbr. skýringu að ofan.)

Eins og sést á línuritinu, þá eru meginvextir SÍ ýmist vanmetnir eða ofmetnir sé miðað við Taylor-regluna.  Þeir fylgja betur rauðu línunni en þeirri bláu.  Spurningin er hins vegar hvað hefði gerst á árunum fyrir hrun, ef þeir hefðu fylgt bláu línunni, þ.e. verðbólgu samkvæmt samræmdri vísitölu.  Meira um það á eftir.

Framleiðsluspenna og jafnvægisraunvextir

Tvær stærðir sem skipta miklu máli varðandi ákvörðun meginvaxta SÍ eru annars vegar framleiðsluspennan og hins vegar jafnvægisraunvextir.  Í hverju einast riti af Peningamálum er framleiðsluspenna fortíðarinnar reiknuð út og spáð fyrir um hver hún verður í framtíðinni (og raunar oft aftur í tímann).  Það er einna helst eins og hagfræðingar SÍ eigi í miklum erfiðleikum með að átta sig á þróun framleiðsluspennu jafnvel nokkur ár aftur í tímann (!), hvað þá að þeir hafi grænan grun um hvernig horfur til framtíðar eru (nema þá mjög grófar).  Svo dæmi sé tekið er í Peningamálum 2009/4 reiknað með að framleiðsluspenna vegna 2012 verði jákvæð um 0,9%.  Í næstu útgáfum Peningamála er spáin um framleiðsluspennu fyrir 2012: -0,2%, -0,5%, -1,2%, -0,6%, -0,6%, -1,5% og -2,2% í Peningamálum 2011/3.  Munar þarna ansi miklu, því helmingur framleiðsluspennunnar reiknast inn í niðurstöðu Taylor-reglunnar. Mismunur upp á 3,1% getur í þessu tilfelli hækkað spá um meginvexti um 1,55%.

Jafnvægisraunvextir eru síðan tala sem Seðlabankinn gefur ekki einu sinni upp í Peningamálum.  A.m.k. fann ég ekki annað en tilvísun í hugtakið án þess að gerð væri nokkur tilraun til að tilgreina hverjir þeir væru.  Þeir eru hins vegar gefnir upp í gagnagrunni fyrir QMM-líkan bankans.  Kemur þar fram að jafnvægisraunvextir voru ákveðnir 4,5% allt fram til 30. september 2008, en lækkaðir niður í 3,0% eftir það.  En hvað eru jafnvægisraunvextir?  Samkvæmt kennsluefni í þjóðhagfræði, þá eru það þeir vextir sem þarf til að koma hagkerfinu í jafnvægi, sem sagt mjög óræð stærð.  Eins og kom fram að ofan, þá eru þeir 3,0% á Íslandi að mati SÍ, en 2,0% í Bandaríkjunum.  Almennt eru þeir hærri í smærri hagkerfum en þeim stærri.

Velta má fyrir sér hvort þessi útreikningur á jafnvægisraunvöxtum sé réttur, þ.e. hvort sömu jafnvægisraunvextirnir eigi við í lítilli verðbólgu og í mikilli.  Nú væri gott að fá skoðun einhvers hagfræðings á því.  Öll breyting á jafnvægisraunvöxtum fer beint inn í niðurstöðu Taylor-reglunnar.  Miðað við að verðbólga, sama hvernig hún er mæld, er undir verðbólgumarkmiðum, þá eru jafnvægisraunvextir upp á 3% vel yfir 100% álag á verðbólgu.  Miðað við nýjustu verðbólgutölur samkvæmt VNV er álagið 1,5 falt og miðað við samræmda vísitölu er álagið 7,5 föld verðbólgan!

Loks má spyrja sig hvort breytingin á meginvöxtum úr veðlánsvöxtum í 7 daga innlánsvexti hefði átt að breyta jafnvægisraunvöxtunum.  Munurinn á þessum tvennum vöxtum er 0,75%.  Er þá hægt að segja með réttu að jafnvægisraunvextirnir séu 3%?  Er ekki réttara að segja þá vera 3,75%?  Er hægt að breyta viðmiðinu fyrir meginvexti án þess að breyta forsendunum sem notaðar eru?  Mér finnst það vera hrein og bein fölsun eða blekking að hliðra viðmiðinu til um 0,75% án þess að breyta forsendum gagna sem Taylor-reglan er fóðruð á.

Hefði notkun SVN við vaxtaákvörðun breytt einhverju?

Maður getur ekki annað en spurt sig hvort það hefði breytt einhverju fyrir hrun og eftir að nota SVN við ákvörðun meginvaxta SÍ í staðinn fyrir VNV.  Bláa línan á grafinu að ofan segir eitt og annað.  Er ekki líklegt að stýrivextir hefðu lækkað árið 2005, ef miðað hefði verið við SVN, í staðinn fyrir að hækka?  Lægri vextir hefðu líklegast dregið úr ásókn í vaxtamunaviðskipti.  Ómögulegt er að segja hvort hægt hefði verið að koma í veg fyrir míníkrísuna árið 2006, en Seðlabankinn hefði þá átt möguleika á að hækka stýrivextina duglega til að sporna að einhverju leiti gegn henni.  Í staðinn gerði bankinn í raun ekkert annað en að láta vextina elta verðbólguna.  Þeir voru ekki notaðir sem það stjórntæki sem þeir eiga að vera.

Annað sem skiptir máli hér er að fólk og fyrirtæki leituðu í gengistryggð lán til að flýja vaxtastefnu Seðlabankans.  Stýrivextir upp á 5% í stað 13,25% hefðu örugglega breytt einhverju. A.m.k. virðist ljóst, að stýrivextir með viðmið í verðbólgu samkvæmt SVN hefðu breytt miklu.

Nú eftir hrun, þá virðist sem Seðlabankinn hafi lækkað stýrivextina heldur hraðar en efni stóðu til.  Frá ársbyrjun 2014 hafa stýrivextir/meginvextir bankans verið hærri en Taylor-reglan segir.  Sé miðað við VNV, þá munar ekki alltaf miklu, en sé miðað við SVN, þá er munurinn umtalsverður.  Mestur fór munurinn í 3% í október og nóvember í fyrra (2014), en minnstur verið 1,6% í ágúst.

Breytingar á húsnæðisverði og verðbólga

Það sem af er þessu ári hafa verið gerðir 7.130 kaupsamningar, samkvæmt frétt Stöðvar 2 í kvöld, þar af var bara hluti af því kaup einstaklinga á eigin húsnæði, gef mér að það hafi verið ríflega helmingur eða 4.000 kaupsamninganna.  Um 100.000 heimili búa í eigin húsnæði sem þýðir að í kringum 4% heimila hafa skipt um húsnæði.  Hækkun húsnæðisverðs hefur því ekki áhrif á hin 96 prósentin fyrir utan hækkun fasteignagjalda.  Við kaup og sölu jafnast hækkun nýs húsnæðis að stórum hluta út á móti hækkun á hinu selda húsnæði.  Þrátt fyrir þetta telur Hagstofan (og þar með Seðlabankinn) að breytingar á húsnæðisverði vegi 14,83% (eða um 1/7) í VNV!  Það er ekki vegna vaxtanna sem fólk greiðir af lánum né afborgana af lánum né verðbótanna sem leggjast á lánin.  Nei, það er vegna þess að húsnæði sem um 4% heimila er að fjárfesta í hefur hækkað í verði.  Ekkert tillit virðist vera tekið til þess á hvaða verði önnur eign var hugsanlega seld á og hvort hún hafi verið seld með miklum hagnaði miðað við kaupverð á sínum tíma.  Hafi ég keypt og selt, þá skiptir mig ekki máli, ef báðar eignir hafi hækkað um 10 m.kr. á einu ári, þó önnur hafi hækkað um 10% en hin um 5%.  Hafi íbúðaskipti þýtt að ég þarf að auka við skuldir mínar um 10 m.kr. fyrir hækkun, þá þarf ég líka að gera það eftir hækkun.

Lokaorð

Kannski hefðu lægri vextir SÍ leitt til meiri framleiðsluspennu vegna ódýrari lána og aukinnar verðbólgu, þar sem gengið hefði ekki styrkst eins mikið.  Það er fullt af efum og kannski í þessu öllu.  En séu menn að nota líkön til að taka mikilvægar ákvarðanir, þá þarf að vera á hreinu hvaða forsendur eru notaðar.  Það má ekki vera á forræði eins aðila að ákveða hvaða verðbólgutölur eru notaðar, hvaða gögn eru notuð, á hvaða forsendum er byggt, að yfirfara niðurstöðurnar og taka út aðferðafræðina.  Ég skil ekki hvers vegna Seðlabanki Íslands metur mjög sambærilega verðbólgu á allt annan hátt en Seðlabanki Evrópu.  Ég skil ekki hvers vegna ECB lækkar vexti sína til að örva hagkerfið og koma af stað verðbólgu, en SÍ hækkar vextina til að kæla hagkerfið, þegar samræmd vísitala neysluverðs mælist 0,1% hjá öðrum og 0,4% hjá hinum.  Loks skil ég ekki hvers vegna Seðlabanki Íslands vill ráðast gegn verðbólgu sem felst í hækkun húsnæðisverðs, þegar ECB og seðlabankar annarra helstu viðskiptalanda okkar gera það ekki.

Kannski er ég á villislóðum í pælingum mínum, en þá þætti mér gott að fá ábendingar um það hvar ég fer út af slóðinni.